his article presents the derivation of the far-field criterion for two fundamental wire-type antennas: electric (or Hertzian) dipole and magnetic dipole.
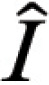 0 = I0, positioned symmetrically at the origin of the coordinate system and oriented along the z-axis.
0 = I0, positioned symmetrically at the origin of the coordinate system and oriented along the z-axis.
The complete fields of the Hertzian dipole, at a distance r from the origin, can be obtained from the vector magnetic potential A shown in Figure 1, (see [1] for the derivations), and can be expressed as, [2],
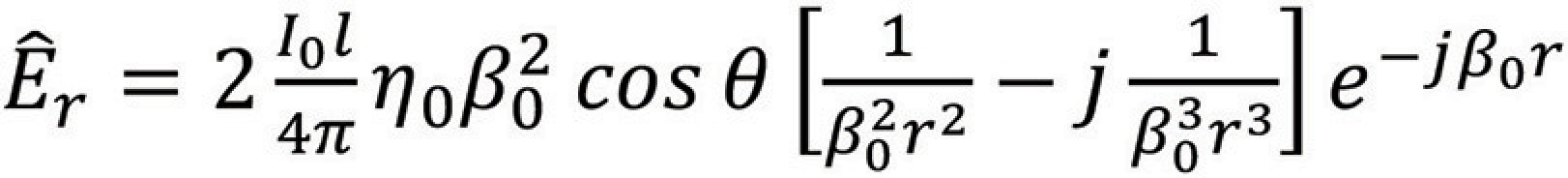
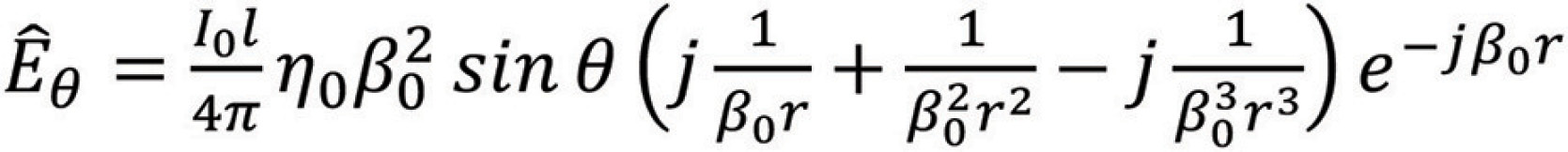
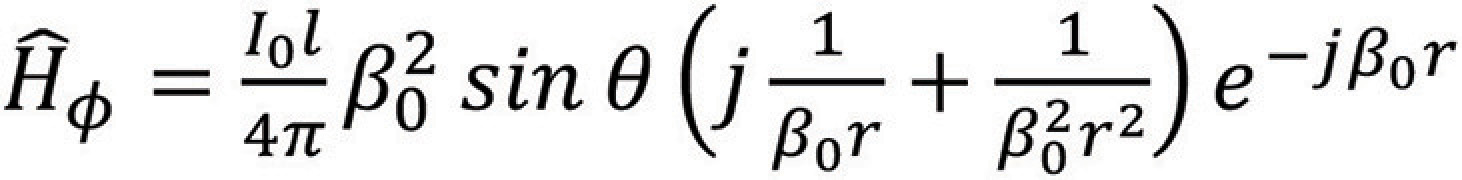
where η0 is the intrinsic impedance of free space, and β0 is the phase constant.
With this electromagnetic wave, we associate wave impedance, defined as

A far-field criterion (distance r from the antenna) for Hertzian dipole (and other wire-type antennas) is derived from the requirement that the magnitude of the wave impedance in far field is equal to the intrinsic impedance of free space.
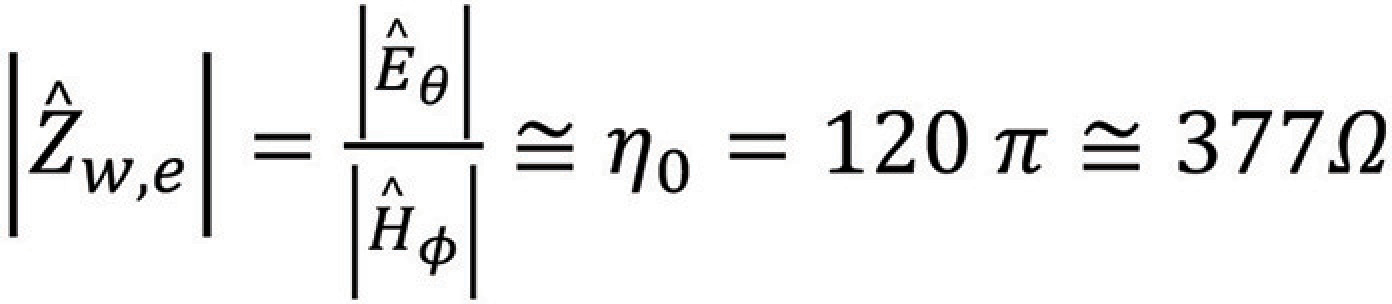
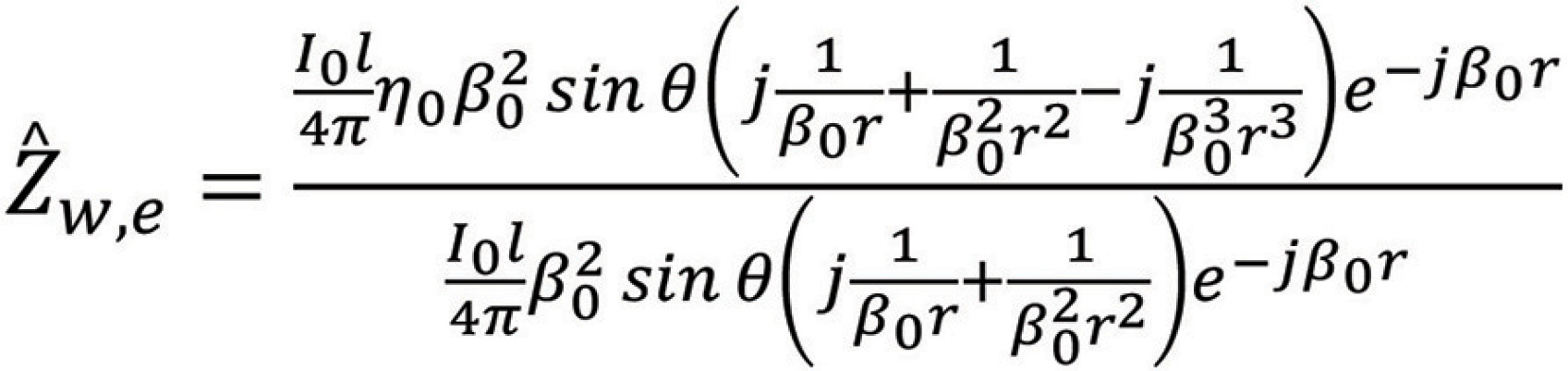
or

Multiplying the numerator and denominator by  we obtain
we obtain

or
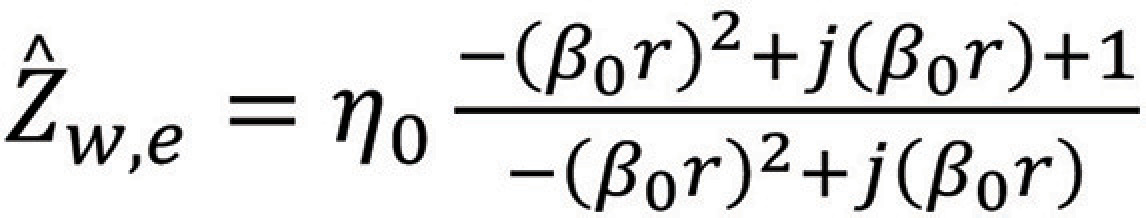

we obtain,
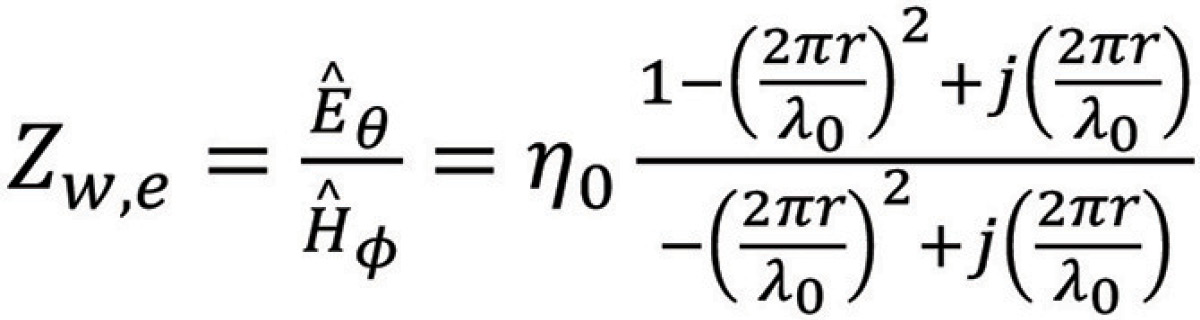
We can evaluate this expression at different distances (in terms of the wavelength) from the antenna, for instance, (r = λ0/2π, r = λ0, r = 3λ0). When evaluated at r = 3λ0, the wave impedance becomes

The result in Eq. (12) leads to the far-field criterion for the Hertzian dipole (and other wire‑type antennas):

 0 = I0, positioned in the xy plane, with the center of the loop at z = 0.
0 = I0, positioned in the xy plane, with the center of the loop at z = 0.
The complete fields of the magnetic dipole, at a distance r can be expressed [2],

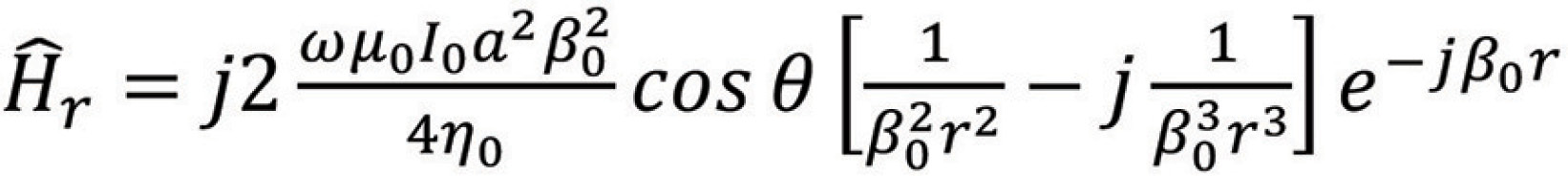

The wave impedance for magnetic dipole is defined as
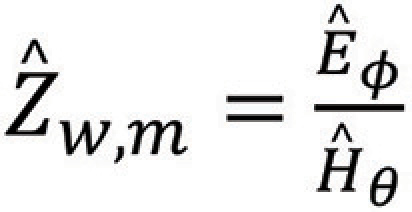
Using Eqns. (2.1) and (2.3) in Eq. (2.4) we get
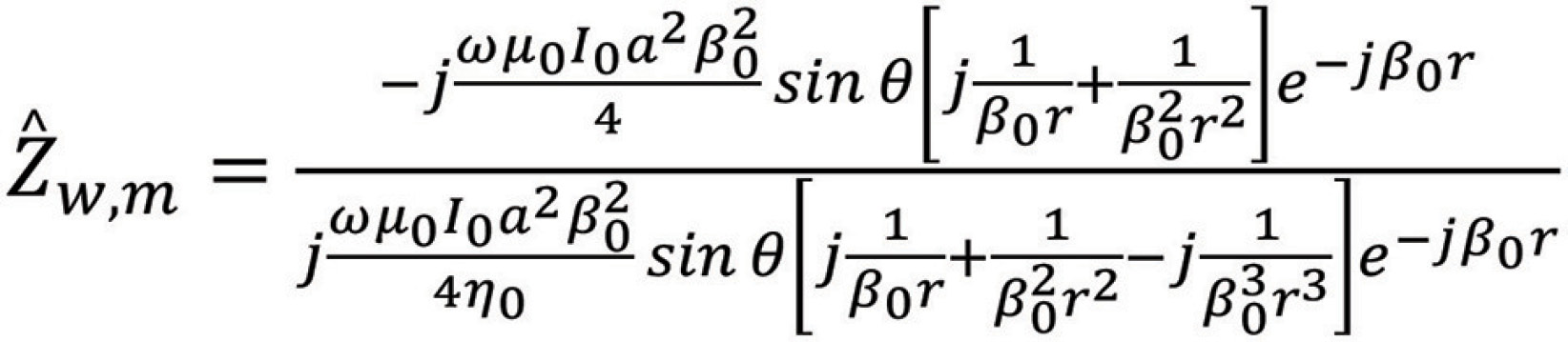
or
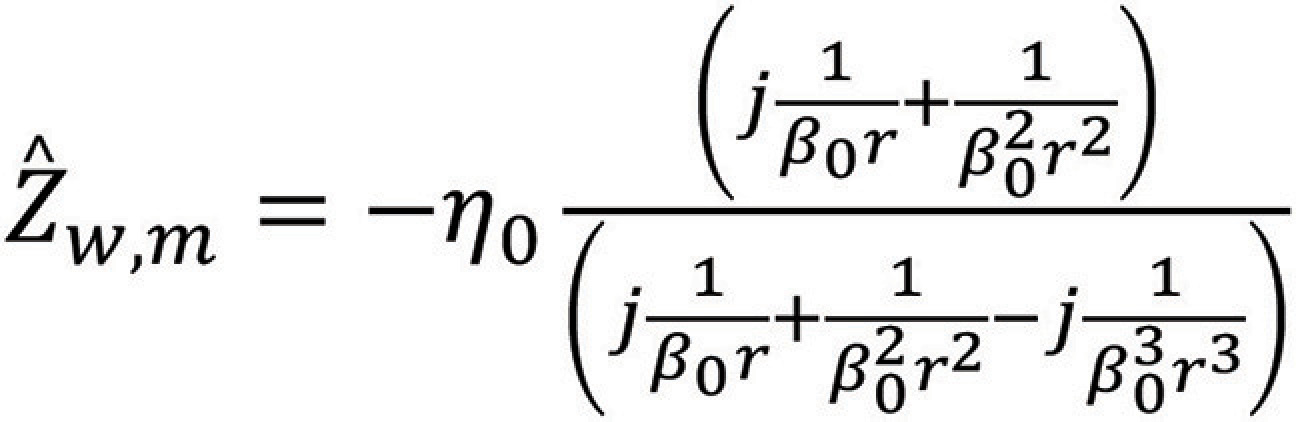
Multiplying the numerator and denominator by  we obtain
we obtain
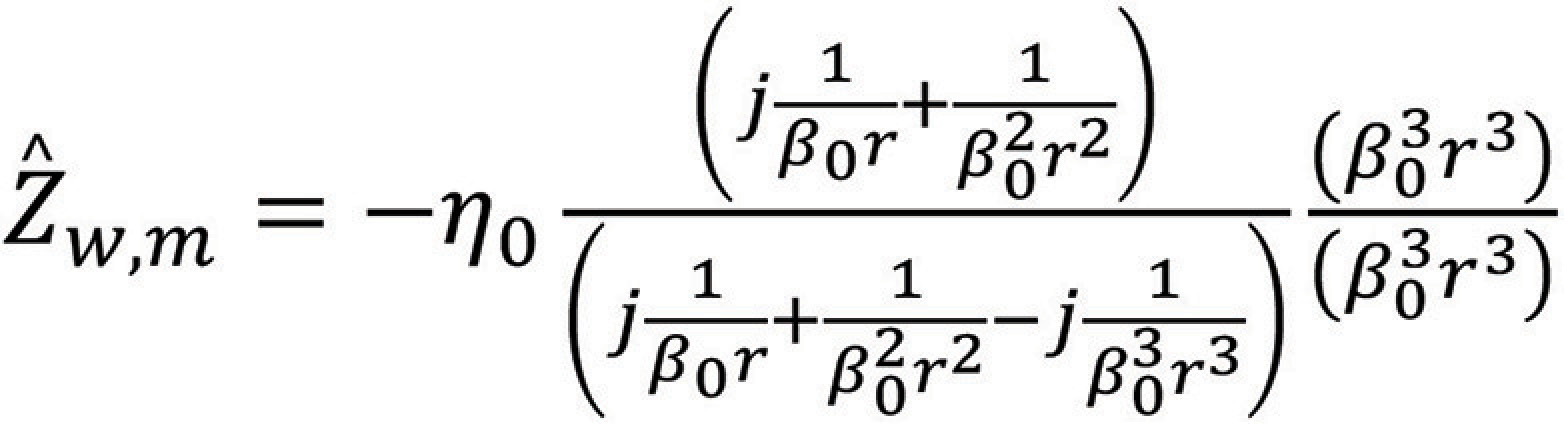
or

Letting,
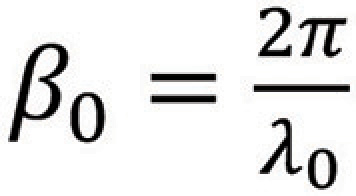
We obtain

Evaluating Eq. (2.10) at r = 3λ0 we get

Thus, the magnitude of the wave impedance

We have arrived again at the far-field criterion as
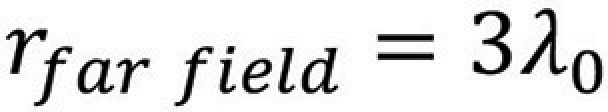
References
- Bogdan Adamczyk, Foundations of Electromagnetic Compatibility with Practical Applications, Wiley, 2017.
- Clayton R. Paul, Introduction to Electromagnetic Compatibility, Wiley, 2006.


