Shielding to Prevent Radiation

EMC concepts explained

Part 2: Uniform Plane Wave Normal Incidence on a Conducting Shield

his is the second of seven articles devoted to the topic of shielding to prevent electromagnetic wave radiation. The first article, [1], discussed the reflection and transmission of uniform plane waves at a normal boundary. This article discusses the normal incidence of a uniform plane wave on a solid conducting shield with no apertures.

Uniform Plane Wave Incident on a Shield in Far Field

Consider a conducting shield of thickness t, conductivity σ, permittivity ε, and permeability µ, surrounded on both sides by air (free space, and thus a perfect dielectric), as shown in Figure 1 [2].

Figure 1: Uniform plane incident on a conducting shield

A uniform plane wave is normally incident on its left interface. Uniformity assumption, together with normal incidence, means that the shield is in the far field of the radiation source.

The incident wave upon arrival at the leftmost boundary () will be partially reflected () and partially transmitted (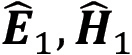) through the shield. The transmitted wave (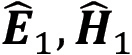) upon arrival at the rightmost boundary will be partially transmitted () through the shield.

The reflected wave (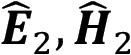) propagates back through the shield and strikes the first interface, incident from the right.

Once again, a portion of this wave is transmitted through the left interface and adds to the total reflected field in the left medium, and a portion is reflected and proceeds to the right.

The process continues in the same fashion, but the additional reflected and transmitted fields are progressively attenuated. If a shield has a thickness that is much greater than the skin depth of the material [3] at the frequency of the incident field, these multiple reflections and transmissions can be disregarded, and only the initial reflection and transmission at the left and right interfaces need to be considered.

The incident wave is described by (since air is treated as a perfect dielectric α₀ = 0 and )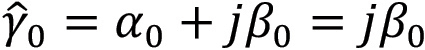

where

The reflected wave is described by

The wave transmitted through the left interface is described by

where

The wave reflected at the right interface is described by

Finally, the transmitted wave through the right interface is described by

Shielding Effectiveness of the Shield in Far Field

The effectiveness of the shield, or shielding effectiveness, SE, can be determined by evaluating the ratio of the incident field magnitude to the transmitted field magnitude.

Since the wave is a uniform wave, the two definitions are identical, since the electric and magnetic field magnitudes are related by the intrinsic impedance of the medium.

Let’s demonstrate that. Recall from the previous article, [1], that the uniform plane wave was described by

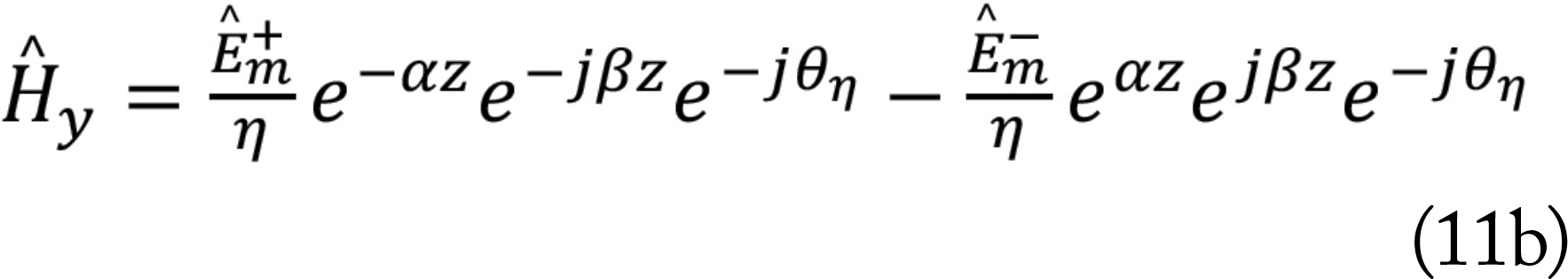
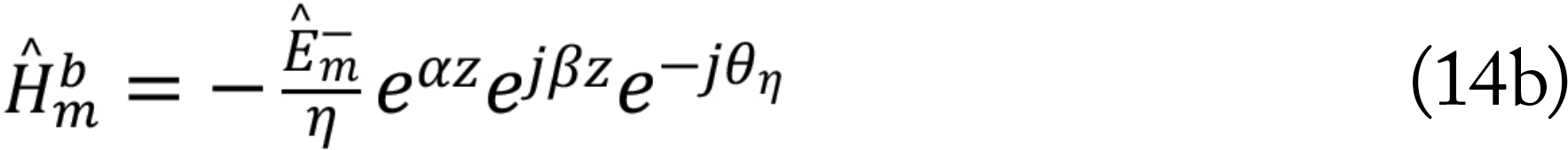
The wave described by Equations (11) consists of the forward and backward propagating waves.

where the forward waves are described by

while the backward waves are described by

Let us concentrate on the forward propagating waves and look at their magnitudes. But before we do that let’s look at a very important and useful Euler’s identity, usually expressed in a manner similar to

and therefore

It might not be apparent from Eq. (15) that Euler’s identity is valid for any argument, whether it has a meaning or not. Just like this one

since

which means that

Now, let’s return to Equations (13) and obtain the magnitudes of the forward propagating uniform plane wave.

Now, let’s determine the ratio of the magnitude of the forward E wave to the magnitude of the forward H wave

Let’s repeat the definition of the shielding effectiveness given by Equations (10), as Equations (23)

and let’s concentrate on Eqn. (23b). The magnitudes of the incident and transmitted forward H waves are related to the magnitudes of the incident and transmitted forward E waves by

Thus,

Which shows that the two definitions of the shielding effectiveness given by Equations (23) are identical. Usually, we use definition in Eq. (23a) and express the shielding effectiveness in decibels. Then, the definition in Equations (24) becomes

The objective of the next articles will be to determine the shielding effectiveness given by Equation (26).

References

Bogdan Adamczyk, “Shielding to Prevent Radiation – Part 1: Uniform Plane Wave Reflection and Transmission at a Normal Boundary,” In Compliance Magazine, June 2025.
Bogdan Adamczyk, Principles of Electromagnetic Compatibility – Laboratory Exercises and Lectures, Wiley, 2023.
Bogdan Adamczyk, “Skin Depth in Good Conductors,” In Compliance Magazine, February 2020.

Share this story:

Dr. Bogdan Adamczyk is professor and director of the EMC Center at Grand Valley State University (http://www.gvsu.edu/emccenter) where he performs EMC educational research and regularly teaches EM/EMC courses and EMC certificate courses for industry. He is an iNARTE-certified EMC Master Design Engineer. He is the author of two textbooks, “Foundations of Electromagnetic Compatibility with Practical Applications” (Wiley, 2017) and “Principles of Electromagnetic Compatibility: Laboratory Exercises and Lectures” (Wiley, 2024). He has been writing “EMC Concepts Explained” monthly since January 2017. He can be reached at adamczyb@gvsu.edu.

Back to Issue