EMC Resonance Part I: Non-Ideal Passive Components

EMC concepts explained

EMC Resonance
Part I: Non-Ideal Passive Components

his article is part of a two-article series devoted to the concept of resonance in EMC. In Part I the fundamental circuit background is presented and illustrated by the resonance phenomenon in the non-ideal models of passive circuit components: capacitors, ferrite beads, resistors, and inductors. Part II (to appear in the next issue) describes the resonance in the decoupling capacitor circuits.

Resonance in RLC Circuits

In circuit courses, the study of resonance is usually limited to the two classical 2^nd-order circuits, series and parallel RLC configurations. These circuits, shown in Figure 1, contain a single lumped capacitor and a single lumped inductor connected either “purely” in series or “purely” in parallel.

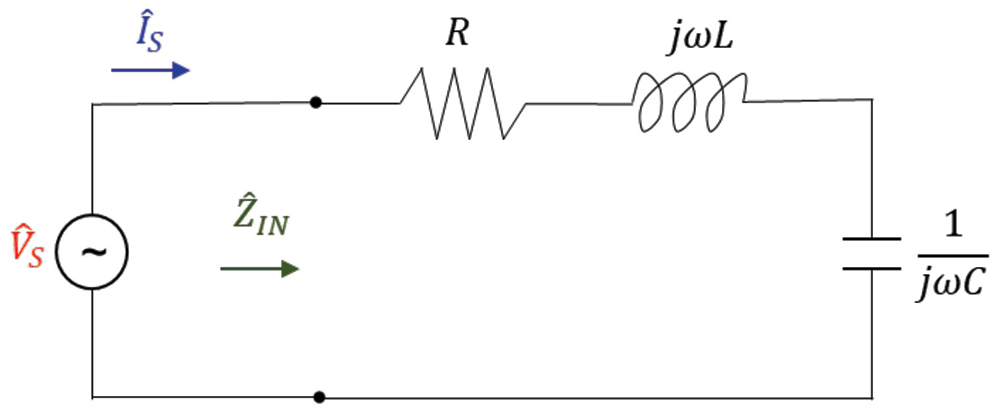
Actual circuits differ from these classical configurations; in addition to the intentional discrete reactive components, they contain distributed parasitic inductances and capacitances. Nevertheless, the study of these basic RLC configurations provides an insight into the more complex topologies and their behavior. Let’s begin with a series RLC circuit.

1. “Pure” Series Resonance – Non-Ideal Capacitor Model

Consider the series RLC resonant circuit shown in Figure 2.

Since the study of resonance is performed in the sinusoidal steady-state, the voltage and current, in Figure 2, are shown in the phasor forms, and the component values are replaced by their impedances [1].

In order to introduce the concept of resonance, let’s calculate the input impedance to the circuit.

When

the input impedance is purely real

Figure 1: The “classical” series and parallel RLC resonant circuits

Figure 2: The series RLC resonant circuit

This happens at the frequency

From the circuit theory, we recognize this frequency as the undamped natural frequency. Let’s look at the consequences of the fact that the input impedance is purely real at that frequency. The voltage and current phasors can be expressed in terms of their magnitudes and angles as

Consequently, the input impedance in Eq. (1.1) can be written as

Since, at ω₀, the input impedance is purely real, it follows that

That is, at ω₀, the voltage and current are in phase! We have arrived at the definition of the resonant frequency:

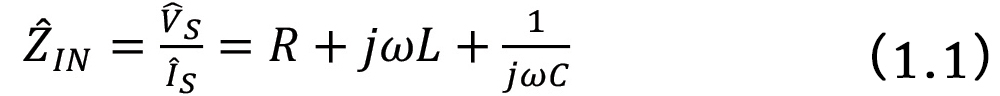
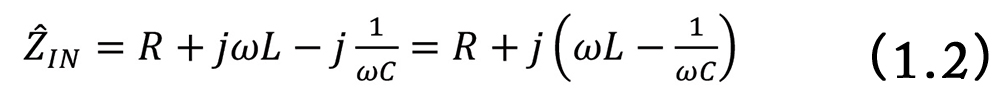
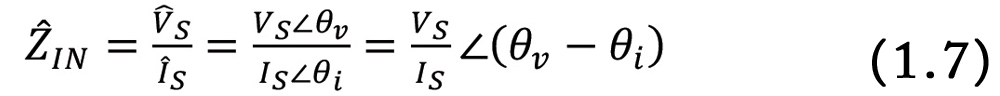
The resonant frequency, ω_r , is a frequency at which the voltage and current phasors are in phase (with respect to the same two terminals of the circuit).

Thus, for the series RLC circuit, the resonant frequency is the same as the undamped natural frequency.

Note: 1) Not every RLC circuit is resonant. 2) When the circuit is resonant, its resonant frequency, in general, is different from ω₀. 3) The “classical” series and parallel circuit configurations are always resonant, and their resonant frequency is the same as ω₀.

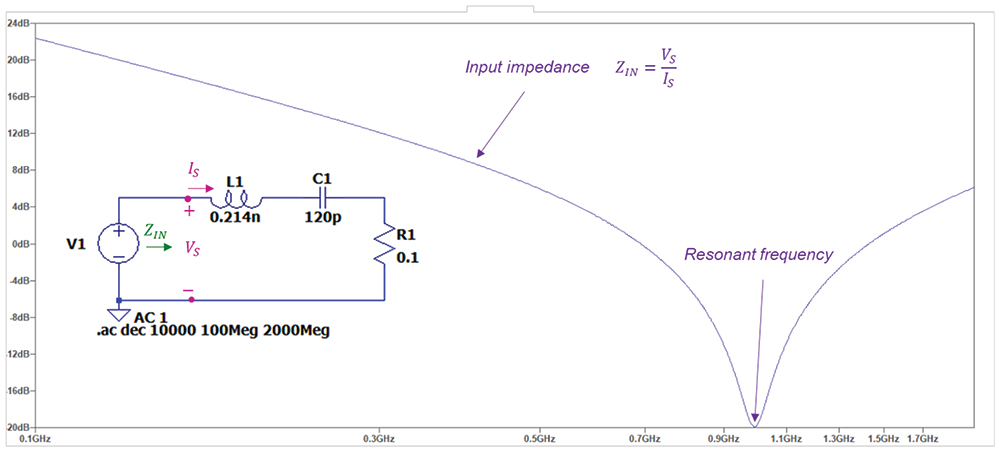
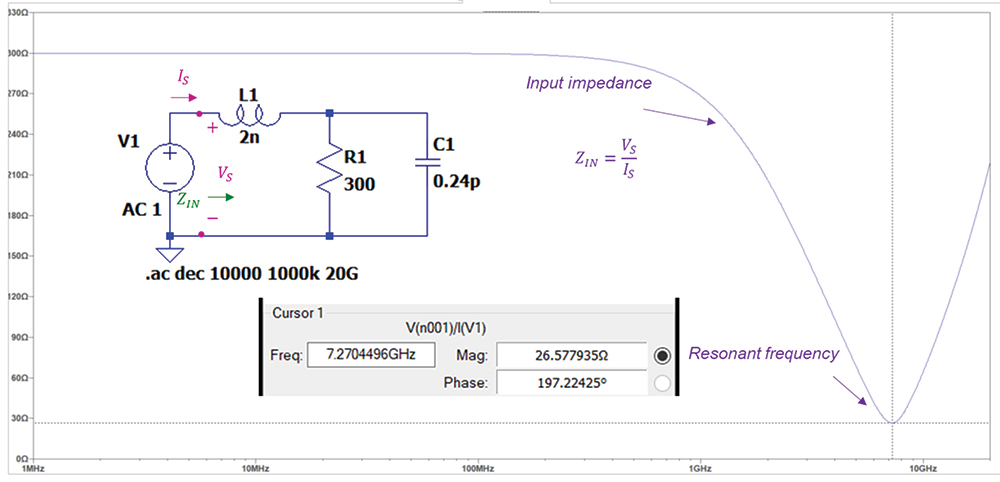
At resonant frequency, the magnitude of the input impedance is minimum. Let’s illustrate this using a circuit model of a nonideal capacitor [2] and plotting its input impedance. This is shown in Figure 3.

2. “Pure” Parallel Resonance – Ferrite Bead Model

Consider the parallel RLC resonant circuit shown in Figure 4.

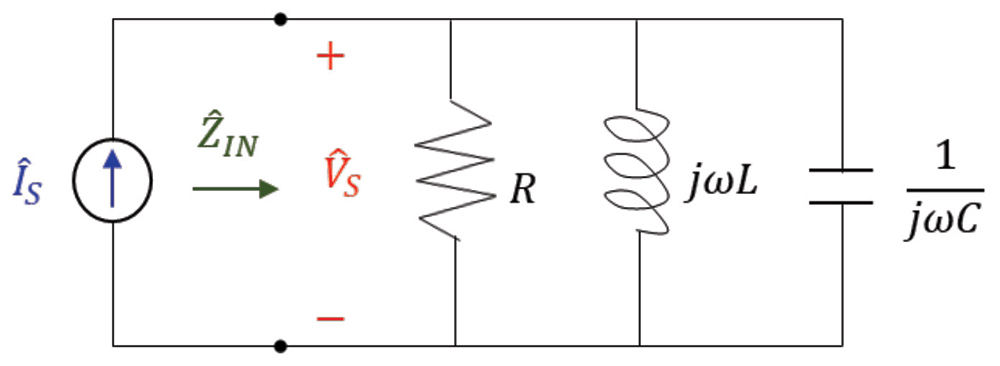
Let’s calculate the input impedance to this circuit.

Thus

When

the input impedance is purely real (voltage and current are in phase) and equal to

Figure 3: Series RLC circuit – Input impedance is minimal at the resonant frequency

Figure 4: The parallel RLC resonant circuit

This happens at the resonant frequency of

Thus, at resonant frequency, the magnitude of the input impedance is maximum. Let’s illustrate this by using a circuit model of ferrite bead [3] and plotting its input impedance. This is shown in Figure 5.

3. “Hybrid” Series Resonance – Non-Ideal Resistor Model

Consider a variation of the series RLC resonant circuit, shown in Figure 6.

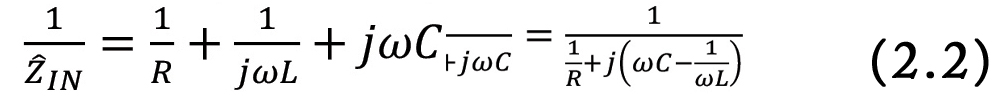
This circuit corresponds to a non-ideal model of a resistor [2]. Let’s calculate the input impedance to the circuit.

Multiplying the numerator and denominator by the complex conjugate of the denominator, and separating the real and imaginary parts, results in

The input impedance is purely real (voltage and current are in phase) when the imaginary part of the impedance is zero, or

Leading to

and resulting in a resonant frequency of

Figure 5: Parallel RLC circuit – Input impedance is maximal at the resonant frequency

Figure 6: “Hybrid” series RLC resonant circuit

Figure 7: “Hybrid” series RLC circuit – Input impedance of a non-ideal resistor

When

The circuit is resonant, and its resonant frequency is different from the undamped natural frequency. To illustrate the circuit behavior at resonance, let’s look at the input impedance of a non-ideal resistor. This is shown in Figure 7.

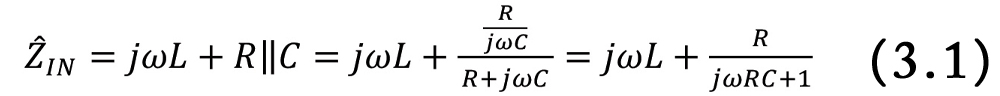
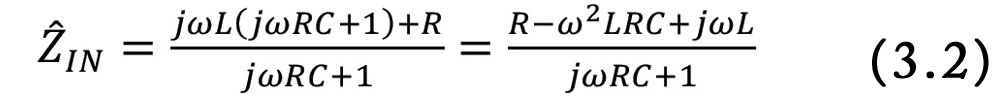
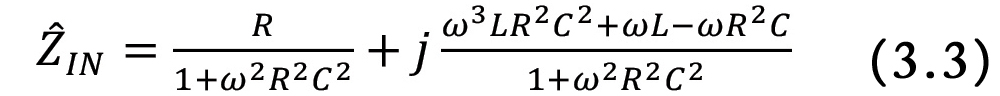
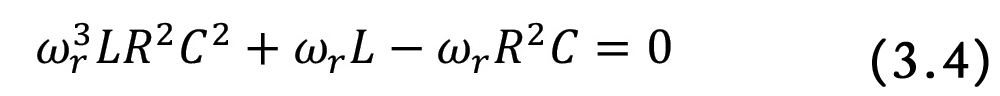
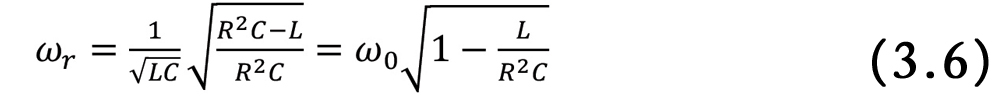
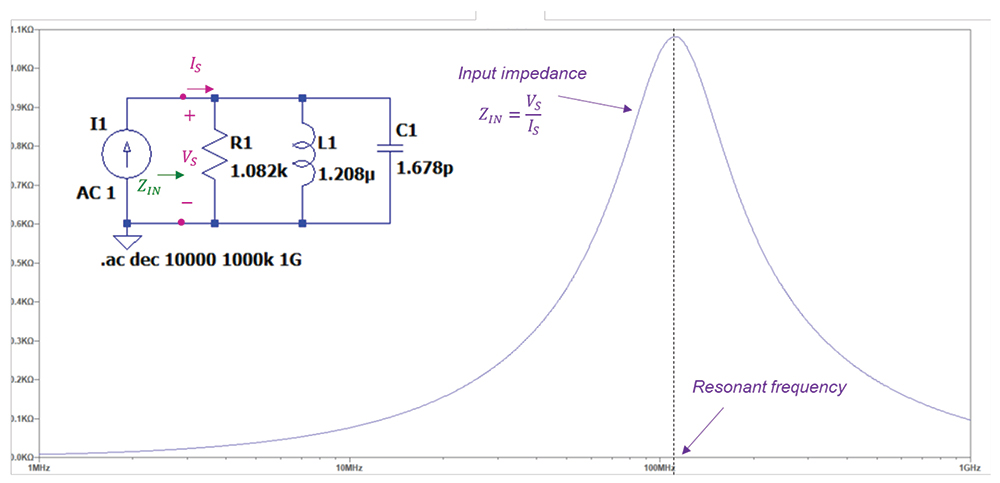
Note: the simulation model in Figure 7 is used only to show that the hybrid series RLC circuit with the component values shown is indeed resonant. This simple model is not valid beyond 2 GHz frequency, and thus, beyond 2 GHz, the simulated impedance plot and the value of the resonant frequency do not reflect the results that would be obtained from the laboratory measurements.

4. “Hybrid” Parallel Resonance – Non-Ideal Inductor Model

Consider the variation of the parallel RLC resonant circuit, shown in Figure 8.

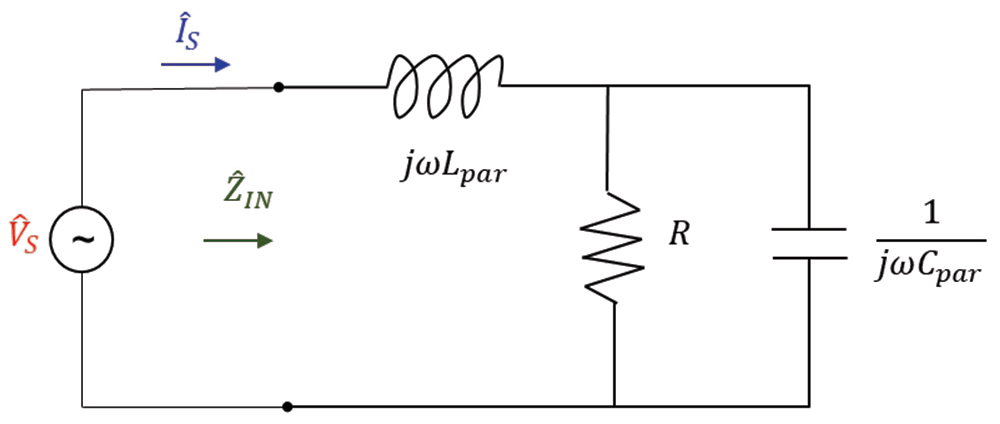
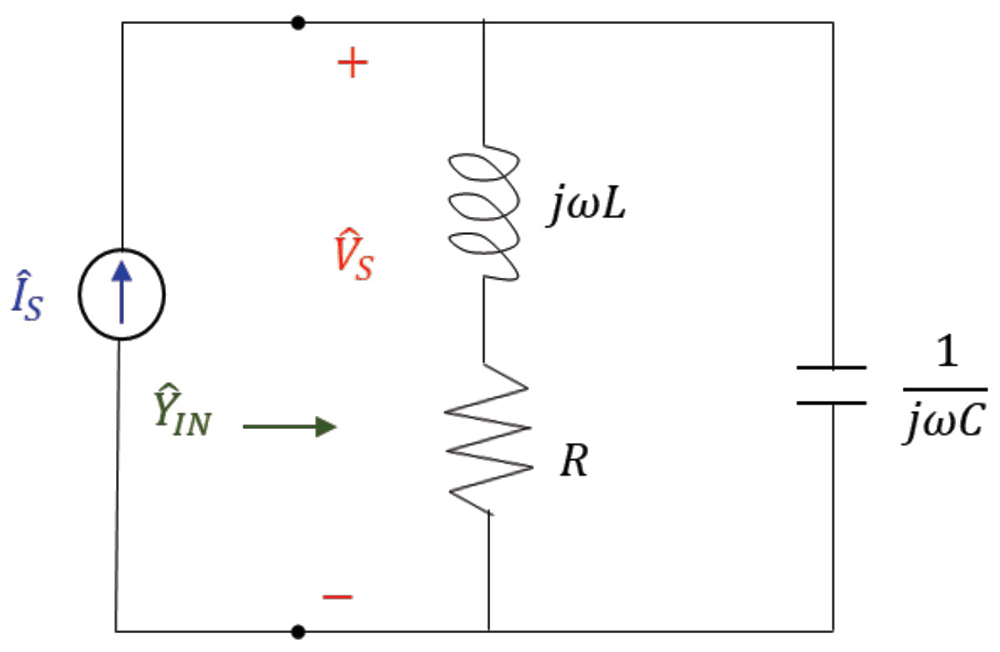
This circuit corresponds to a non-ideal model of an inductor [2]. Let’s calculate the input admittance to the circuit.

Resonance occurs when the admittance is real, or

and thus

From Eq. (4.3), we get

Resulting in a resonant frequency of

When

The circuit is resonant, and its resonant frequency is again different from the undamped natural frequency. To illustrate the circuit behavior at resonance, let’s look at the input impedance of a non-ideal inductor. This is shown in Figure 9.

Figure 8: “Hybrid” parallel RLC resonant circuit

Figure 9: “Hybrid series RLC circuit – Input impedance of a non-ideal inductor

References

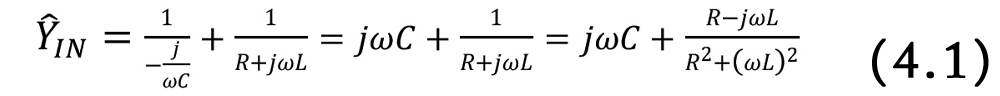
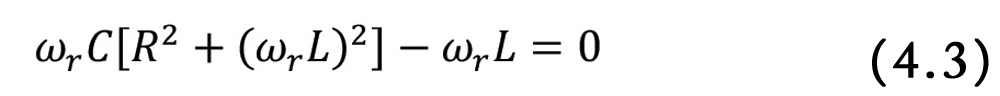
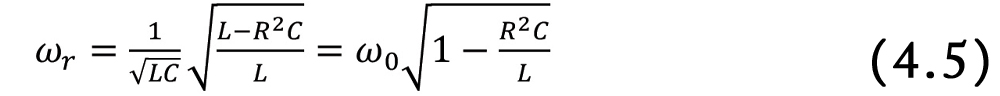
Bogdan Adamczyk, Foundations of Electromagnetic Compatibility with Practical Applications, Wiley, 2017.
Adamczyk, B., Teune, J., “Impedance of the Four Passive Circuit Components: R, L, C, and a PCB Trace,” In Compliance Magazine, January 2019.
https://www.analog.com/en/analog-dialogue/articles/ferrite-beads-demystified.html

Share this story:

Dr. Bogdan Adamczyk is professor and director of the EMC Center at Grand Valley State University (http://www.gvsu.edu/emccenter) where he regularly teaches EMC certificate courses for industry. He is an iNARTE certified EMC Master Design Engineer. Prof. Adamczyk is the author of the textbook “Foundations of Electromagnetic Compatibility with Practical Applications” (Wiley, 2017) and the upcoming textbook “Principles of Electromagnetic Compatibility with Laboratory Exercises” (Wiley 2022). He can be reached at adamczyb@gvsu.edu.

Back to Issue